Examples of Graph Analysis#
This section provides three examples of how to perform graph analysis with EasyGraph.
To analyze and draw Structural Hole Spanners on the karate club dataset with EasyGraph#
>>> from easygraph.datasets import get_graph_karateclub
>>> import easygraph as eg
>>> G = get_graph_karateclub()
>>> # Calculate five shs(Structural Hole Spanners) in G
>>> shs = eg.common_greedy(G, 5)
>>> # Draw the Graph, and the shs is marked by a red star
>>> eg.draw_SHS_center(G, shs)
>>> # Draw CDF curves of "Number of Followers" of SH spanners and ordinary users in G.
>>> eg.plot_Followers(G, shs)
Fundamentals of Graph Properties and Operations#
Import EasyGraph, and start with an undirected graph G:
>>> import easygraph as eg
>>> G=eg.Graph()
Add edge (1,2) to the graph:
>>> G.add_edge(1,2)#Add a single edge
>>> G.edges
[(1, 2, {})]
Add more edges to the graph:
>>> G.add_edges([(2, 3), (1, 3), (3, 4), (4, 5)])#Add edges
>>> G.edges
[(1, 2, {}), (1, 3, {}), (2, 3, {}), (3, 4, {}), (4, 5, {})]
Add a node with attributes:
>>> G.add_node('hello world')
>>> G.add_node('Jack', node_attr={
... 'age': 10,
... 'gender': 'M'
... })
>>> G.nodes
{1: {}, 2: {}, 3: {}, 4: {}, 5: {},
'hello world': {},
'Jack': {
'age': 10,
'gender': 'M'
}
}
Remove nodes:
>>> G.remove_nodes(['hello world','Tom','Lily','a','b'])#remove edges
>>> G.nodes
{1: {}, 2: {}, 3: {}, 4: {}, 5: {}}
Remove edges:
>>> G.remove_edge(4,5)
>>> G.edges
[(1, 2, {}), (1, 3, {}), (2, 3, {}), (3, 4, {})]
Advanced Python properties:
>>> print(len(G))#__len__(self)
5
>>> for x in G:#__iter__(self)
... print(x)
1
2
3
4
5
>>> print(G[1])# return list(self._adj[node].keys()) __contains__ __getitem__
{2: {}, 3: {}}
Neighbors of node 2:
>>> for neighbor in G.neighbors(node=2):
... print(neighbor)
...
1
3
Add weighted edges:
>>> G.add_edges([(1,2), (2, 3),(1, 3), (3, 4), (4, 5)], edges_attr=[
... {
... 'weight': 20
... },
... {
... 'weight': 10
... },
... {
... 'weight': 15
... },
... {
... 'weight': 8
... },
... {
... 'weight': 12
... }
... ])#add weighted edges
>>> G.add_node(6)
>>> G.edges
[(1, 2, {'weight': 20}), (1, 3, {'weight': 15}), (2, 3, {'weight': 10}), (3, 4, {'weight': 8}), (4, 5, {'weight': 12})]
>>> G.nodes
{1: {}, 2: {}, 3: {}, 4: {}, 5: {}, 6: {}}
>>> G.adj
{1: {2: {'weight': 20}, 3: {'weight': 15}}, 2: {1: {'weight': 20}, 3: {'weight': 10}}, 3: {2: {'weight': 10}, 1: {'weight': 15}, 4: {'weight': 8}}, 4: {3: {'weight': 8}, 5: {'weight': 12}}, 5: {4: {'weight': 12}}, 6: {}}
Degree and weighted Degree:
>>> G.degree()
{1: 35, 2: 30, 3: 33, 4: 20, 5: 12, 6: 0}
>>> G.degree(weight='weight')
{1: 35, 2: 30, 3: 33, 4: 20, 5: 12, 6: 0}
Transform each node’s value to its index:
>>> G_index_graph, index_of_node, node_of_index = G.to_index_node_graph()
>>> G_index_graph.adj
{0: {1: {'weight': 20}, 2: {'weight': 15}}, 1: {0: {'weight': 20}, 2: {'weight': 10}}, 2: {0: {'weight': 15}, 1: {'weight': 10}, 3: {'weight': 8}}, 3: {2: {'weight': 8}, 4: {'weight': 12}}, 4: {3: {'weight': 12}}, 5: {}}
>>> index_of_node
{1: 0, 2: 1, 3: 2, 4: 3, 5: 4, 6: 5}
>>> node_of_index
{0: 1, 1: 2, 2: 3, 3: 4, 4: 5, 5: 6}
Deep copy of a given graph:
>>> G1 = G.copy()
>>> G1.adj
{1: {2: {'weight': 20}, 3: {'weight': 15}}, 2: {1: {'weight': 20}, 3: {'weight': 10}}, 3: {1: {'weight': 15}, 2: {'weight': 10}, 4: {'weight': 8}}, 4: {3: {'weight': 8}, 5: {'weight': 12}}, 5: {4: {'weight': 12}}, 6: {}}
A subgraph of given nodes:
>>> G_sub = G.nodes_subgraph(from_nodes = [1,2,3])
>>> G_sub.adj
{1: {2: {'weight': 20}, 3: {'weight': 15}}, 2: {1: {'weight': 20}, 3: {'weight': 10}}, 3: {1: {'weight': 15}, 2: {'weight': 10}}}
Egonetwork graph of given node:
>>> ego_network = G.ego_subgraph(center=1)
>>> ego_network.adj
{2: {1: {'weight': 20}, 3: {'weight': 10}}, 1: {2: {'weight': 20}, 3: {'weight': 15}}, 3: {2: {'weight': 10}, 1: {'weight': 15}}}
Connected components:
>>> eg.number_connected_components(G)
2
>>> eg.connected_components(G)
[{6}, {1, 2, 3, 4, 5}]
>>> eg.connected_component_of_node(G, node=3)
{1, 2, 3, 4, 5}
Detection of Structural Hole Spanners#
Use MaxD for structural hole spanners detection:
>>> M=eg.get_structural_holes_MaxD(G,
... k = 5, # To find the top five structural holes spanners.
... C = [frozenset([1,2,3]), frozenset([4,5,6])] # Two communities
... )
>>> M
[3, 1, 2, 4, 5]
Use HAM for structural hole spanners detection:
>>> top_k_nodes, SH_score, cmnt_labels=eg.get_structural_holes_HAM(G,
... k = 2,
... c = 2,
... ground_truth_labels = [[0], [0], [1], [1], [1]]
... )
AMI
HAM: 1.0
HAM_all: 0.25126693574443504
NMI
HAM: 1.0
HAM_all: 0.43253806776631243
Entropy
HAM: 0.0
HAM_all: 0.38190850097688767
>>> top_k_nodes
[4, 3]
>>> SH_score
{1: 2, 2: 1, 3: 3, 4: 4, 5: 0}
>>> cmnt_labels
{1: 2, 2: 2, 3: 2, 4: 1, 5: 1}
Apply the common greedy algorithm for detecting structural hole spanners:
>>> T=eg.common_greedy(G,
... k = 3,
... c = 1.0,
... weight = 'weight')
>>> T
[3, 5, 2]
Generate a sample graph from the Karate Club dataset:
>>> G=eg.datasets.get_graph_karateclub()
Calculate Burt’s metrics for structural hole spanners
Betweenness of node 3:
>>> eg.ego_betweenness(G,3)
6.5
Effective size of all nodes:
>>> eg.effective_size(G)
{1: 11.75, 2: 4.333333333333333, 3: 5.8, 4: 0.666666666666667, 5: -0.3333333333333335, 6: 0.5, 7: 0.5, 8: -1.0, 9: 1.0, 10: 0.0, 11: -0.3333333333333335, 12: -1.0, 13: -1.0, 14: 0.5999999999999996, 15: -1.0, 16: -1.0, 17: -1.0, 18: -1.0, 19: -1.0, 20: 0.3333333333333335, 21: -1.0, 22: -1.0, 23: -1.0, 24: 1.4, 25: 0.3333333333333335, 26: 0.3333333333333335, 27: -1.0, 28: 1.5, 29: 0.3333333333333335, 30: 0.0, 31: 0.5, 32: 3.0, 33: 7.833333333333333, 34: 13.235294117647058}
Efficiency of all nodes:
>>> eg.efficiency(G)
{1: 0.734375, 2: 0.48148148148148145, 3: 0.58, 4: 0.11111111111111116, 5: -0.11111111111111116, 6: 0.125, 7: 0.125, 8: -0.25, 9: 0.2, 10: 0.0, 11: -0.11111111111111116, 12: -1.0, 13: -0.5, 14: 0.11999999999999993, 15: -0.5, 16: -0.5, 17: -0.5, 18: -0.5, 19: -0.5, 20: 0.11111111111111116, 21: -0.5, 22: -0.5, 23: -0.5, 24: 0.27999999999999997, 25: 0.11111111111111116, 26: 0.11111111111111116, 27: -0.5, 28: 0.375, 29: 0.11111111111111116, 30: 0.0, 31: 0.125, 32: 0.5, 33: 0.6527777777777778, 34: 0.7785467128027681}
Constraint of all nodes:
>>> eg.constraint(G)
{1: 0.15542329764660495, 2: 0.27953510802469134, 3: 0.18517663966049389, 4: 0.39665964720507535, 5: 0.5294174382716048, 6: 0.4774848090277778, 7: 0.4774848090277778, 8: 0.4427115885416667, 9: 0.3036007136678201, 10: 0.5, 11: 0.5294174382716048, 12: 1.0, 13: 0.6225043402777779, 14: 0.32333541666666676, 15: 0.5736795943867743, 16: 0.5736795943867743, 17: 0.78125, 18: 0.590868537808642, 19: 0.5736795943867743, 20: 0.37371935013717417, 21: 0.5736795943867743, 22: 0.590868537808642, 23: 0.5736795943867743, 24: 0.30582372164552096, 25: 0.4598765432098765, 26: 0.4598765432098765, 27: 0.6709018166089966, 28: 0.2850692041522491, 29: 0.3869131530607885, 30: 0.44940900134563627, 31: 0.3460064638600538, 32: 0.24457540369088812, 33: 0.2492233622751933, 34: 0.15641868512110732}
Hierarchy of all nodes:
>>> eg.hierarchy(G)
{1: 0.08754463683694338, 2: 0.1544986992144599, 3: 0.04535921163684897, 4: 0.061067624090107915, 5: 0.07134469342227538, 6: 0.035305086439308436, 7: 0.03530508643930843, 8: 0.0011300905133206085, 9: 0.012305615918292673, 10: 0.0, 11: 0.07134469342227538, 13: 0.006282226820057121, 14: 0.01352163842686084, 15: 0.00037766424272729984, 16: 0.00037766424272729984, 17: 0.0, 18: 0.0014421896477064891, 19: 0.00037766424272729984, 20: 0.0033488184456886283, 21: 0.00037766424272729984, 22: 0.0014421896477064891, 23: 0.00037766424272729984, 24: 0.036897065903971515, 25: 0.024311482691998648, 26: 0.024311482691998648, 27: 0.01960343310353982, 28: 0.0086202479405721, 29: 0.007513545360870802, 30: 0.06689992156538088, 31: 0.01286931837997609, 32: 0.020491542893317758, 33: 0.3259402254099858, 34: 0.2416086531756689}
Optimizing performance with C++#
The GraphC class contains most key operations included in the Graph class. e.g. add_node(), add_edges()
EasyGraph also provides three crucial network analysis functions implemented in C++ - multi_source_dijkstra() - betweenness_centrality() - closeness_centrality() - k_core()
Basics of GraphC#
Import EasyGraph and initialize a directed graph G_c :
>>> import easygraph as eg
>>> G_c=eg.DiGraphC()
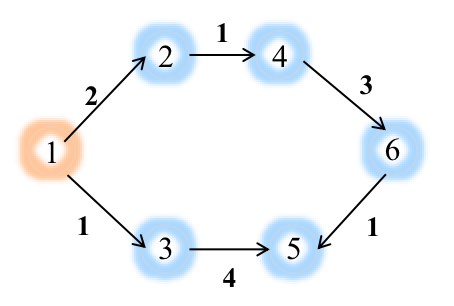
Add edges [(1,2), (2,4), (4,6), (6,5), (3,5), (1,3)] to the graph:
>>> G_c.add_edges([(1,2), (2,4), (4,6), (6,5), (3,5), (1,3)],[{'weight': 2},{'weight': 1},{'weight': 3},{'weight': 1},{'weight': 4},{'weight': 1},])#Add edges with the corresponding edge weights
>>> G_c.edges
[(3, 5, {'weight': 4.0}), (6, 5, {'weight': 1.0}), (4, 6, {'weight': 3.0}), (2, 4, {'weight': 1.0}), (1, 3, {'weight': 1.0}), (1, 2, {'weight': 2.0})]
Retrieve Nodes’ indices:
>>> G_c.node_index # We assign each node a unique id which starts from 0 to n-1 ( n is the number of nodes in your graph)
{1: 0, 2: 1, 4: 2, 6: 3, 5: 4, 3: 5}
Apply the multi_source_dijkstra algorithm with source node 1:
>>> eg.multi_source_dijkstra(G_c, sources=[1], weight="weight") #
[[0.0, 2.0, 3.0, 6.0, 5.0, 1.0]] # The results are returned in the form of nested lists according to the node index from 0 to n-1, where the values of the sublist refer to the shortest paths from source node `1` to other nodes in the graph
Calculating betweenness centrality and closeness centrality:
>>> eg.betweenness_centrality(G_c)
[0.0, 2.0, 3.0, 2.0, 0.0, 1.0]
>>> eg.closeness_centrality(G_c)
[0.0, 0.10000000149011612, 0.20000000298023224, 0.13846154510974884, 0.2631579041481018, 0.20000000298023224]
The k-core function:
>>> eg.k_core(G_c)
[2, 1, 1, 1, 0, 1]
The PageRank algorithm:
>>> eg.pagerank(G_c)
[0.07353112885883649, 0.10478166923491646, 0.16259530606176315, 0.2117369675241203, 0.3425732590854471, 0.10478166923491646]
Usage
The calling syntax and parameter passing of class methods follow the conventions of Python.
For module functions, EasyGraph executes specific code depending on the class of the graph.
